图论方向琐记
1. 无向图包含每个点的最小(边)简单环
有基于分治的 $O(n^3 \log n)$ 做法,此处略去。
有以下重要结论:
对于每个点 $p$ 建以 $p$ 为根的最短路树,我们只需考虑两端点 $\text{LCA}$ 为 $p$ 的非树边 $(u,v,w)$,用 $dis_u+dis_v+w$ 更新答案即可。
证明:
我们称上述边是「跨色边」,其余边是「同色边」。容易发现,一个包含根的边简单环至少经过一条跨色边,否则根连向某个子树的树边至少会经过两次。
对于每条跨色边,注意到 $dis_u$ 的路径和 $dis_v$ 路径一定分属根的两个子树(或其中之一是根),并且只经过一条非树边,故一定没有经过重复的边;同时由最短路树的性质可得包含这条跨色边的环,环长一定不小于 $dis_u+dis_v+w$。$\square$
2. DAG 删点最长路
题意:给定一张 DAG,对于每个点,求出其删掉这个点后(全局)最长路。
考虑枚举删掉的点 $p$。注意到,任意一条(合法)路径一定是下列三者之一:
- 路径上所有点拓扑序都在 $p$ 前面。
- 路径上所有点拓扑序都在 $p$ 后面。
- 路径上存在两个相邻点 $(u,v)$,满足 $u$ 及以前的点拓扑序都在 $p$ 前面,$v$ 及以后的点拓扑序都在 $p$ 后面。
前两种情况可以方便预处理;对于第三种情况,考虑通过 $u\rightarrow v$ 这条边统计,相当于拓扑序上一段区间对一个数 chkmax,也是可以做的。复杂度 $O(n \log n)$。
3. 无向图删边最短路
题意:给定一张无向正权图 $G$,对图上的每条边,求删去该边后 $1 \rightsquigarrow n$ 的最短路。
记 $dis_{x,y}$ 为 $(x,y)$ 之间最短路。
假设删去边 $e=(i,j,k)$ 在 最短路树 $1 \rightsquigarrow n$ 的路径 $P$ 上。(不在的情况一定不会影响答案)
枚举每条 不在 最短路上的边 $(u,v,w)$(注意一条边可以从两个方向经过),若 $1 \rightsquigarrow u$ 和 $v \rightsquigarrow n$ 都不经过 $e$,则经过这条边的 $1 \rightsquigarrow n$ 路径长度必然不小于 $dis_{1,u}+w+dis_{v,n}$ 且一定合法,更新答案。称这样的边 $(u,v,w)$ 为 关键边。
下面只需要说明,删去 $e$ 后一定经过一条关键边。
不妨假设 $P$ 上经过 $e$ 的方向是 $i \rightarrow j$。
记 $T_1,T_n$ 分别为以 $1,n$ 为根的最短路树,并钦定 $P \in T_1 \cap T_n$。
记 $A_i, A_j, B_i, B_j$ 分别为 $T_1$ 上 $j$ 子树以外部分、$T_1$ 上 $j$ 子树,$T_n$ 上 $i$ 子树、$T_n$ 上 $i$ 子树以外部分。
有引理:$A_j \cap B_i = \varnothing$。
证明:
考虑反证。
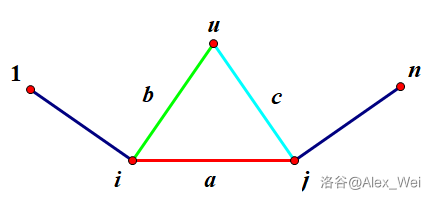
$$\small\text{图源 Alex\_Wei。}$$
假设 $u \in A_j \cap B_i$,则有 $1 \rightsquigarrow i \rightsquigarrow j \rightsquigarrow u$ 和 $u \rightsquigarrow i \rightsquigarrow j \rightsquigarrow n$ 分别为 $1 \rightsquigarrow u$ 和 $u \rightsquigarrow n$ 的最短路,整理得 $a+c \le b \land a + b \le c$,故 $a \le 0$,与正权性矛盾。$\square$
注意证明中需要用到 $G$ 是无向图的性质,对于有向图我们并不存在一个简易高效的确定性算法解决这一问题。(非确定性算法可以见 EI 博客)
有了这一引理后,考虑取出最后一条从 $A_i$ 走到 $A_j$ 的边;由于 $1 \in A_i \land n \in A_j$ 因此这样的边一定存在,不妨记其为 $e'=(u',v',w')$。由于 $A_j \cap B_i = \varnothing$,必有 $v' \in B_j$,因此 $e'$ 是关键边。$\square$
所以我们只要枚举每一条关键边,其可以对 $P$ 上一段区间的被删边产生贡献,使用数据结构维护区间 chkmin 即可。
4
没有奇环的有向图,每个 SCC 都看作无向图后,都没有奇环(即每个 SCC 看作无向图后都是二分图)。
证明:
假设存在一个 SCC 看作无向图后存在一个奇环 $C$,其中 $x$ 条边在有向图中是正的,$y$ 条是反的。
- $x$ 为偶数,$y$ 为奇数:
对于每条反边 $u\rightarrow v$,在原图上必然存在一条路径 $u \leadsto v$ 和一条边 $v\rightarrow u$,由于原图不存在奇环,$u \leadsto v$ 长度必然是奇数,因此将 $C$ 中所有反边都换成原图中对应的路径即可得到原图中存在奇环,矛盾。
- $x$ 为奇数,$y$ 为偶数
同理,将 $C$ 中所有反边都换成原图中对应的路径也可得到原图中存在奇环,矛盾。