基本子串结构学习笔记
前置知识:SAM。
免责声明:本文中略过了很多证明。
引入
考虑如下问题:
(杭电多校 2024 第三场 T6)给定一个字符串 $S$,每次询问一段子串 $S[l\dots r]$,求:
- 有多少个本质不同的字符串 $T$ 满足 $\text{occ(T)}=\text{occ}(S[l\dots r])$,且 $S[l\dots r]$ 是 $T$ 的子串。
- 有多少个本质不同的字符串 $T$ 满足 $\text{occ(T)}=\text{occ}(S[l\dots r])$,且 $T$ 是 $S[l\dots r]$ 的子串。
其中 $\text{occ}(T)$ 表示 $T$ 在 $S$ 中的出现次数。
$|S|,q \le 5\times10^5$,强制在线。
容易想到对于正反串分别建立 SAM,但这样并不是很利于刻画“$\text{occ}$ 等价类”,因为我们并不知道正串 SAM 上的节点跑到反串 SAM 上是哪里。
我们需要一个更有力的、刻画子串的结构。
$\text{ext}$ 等价类与对称压缩 SAM
在思考需要的结构之前,我们要先明确这个所谓的“$\text{occ}$ 等价类”到底长什么样。
Definition 1. 定义 $\text{ext}(T)$ 为极长的串 $T'$ 满足 $\text{occ}(T')=\text{occ}(T)$,且 $T$ 为 $T'$ 的子串。
可以证明,$T'$ 存在且唯一。(注意到 $T'$ 其实就是正串 SAM 上 $T$ 对应节点中最长串与反串 SAM 对应节点中的最长串拼接而成。)
我们称 $T_0,T_1$ 属于一个等价类,当且仅当 $\text{ext}(T_0)=\text{ext}(T_1)$。
我们发现 SAM 已经完成了向左扩展的任务。容易注意到,一个节点可以向右扩展,且不改变其出现次数,当且仅当:
- 它不对应一个后缀。
- 它在 SAM 上的出边(转移边)只有一条。
于是我们可以将出度为 $1$ 且不代表后缀的点与它出边指向的点合并,得到了一个“双向扩展,单向转移”的结构,我们称之为压缩 SAM。压缩 SAM 上的一个点对应一个 $\text{ext}$ 等价类。
好了我们现在可以合并了,因为 $\text{ext}$ 等价类与这个串是正向的还是反向的没有关系。
叠合正反串压缩 SAM 的对应节点,同时保留对应出边,我们得到了一个支持双向转移的结构——对称压缩 SAM。
听起来很有意思。
阶梯划分,基本子串结构
对称压缩 SAM 只刻画了等价类之间的转移关系,等价类内的关系是混乱的,我们考虑把它画到网格图上。
对于每个子串 $S[l\dots r]$,我们将其写在 $(l,r)$ 上;对于同一等价类,我们将其染上同一种颜色。
这样得到的结构就称之为(初步的)基本子串结构或者叫“阶梯划分”,每个同色连通块称为一个块。容易发现块与块之间两两不相交;每个子串只会出现在一种颜色的块内。
下图展示了 $\mathtt{abbab}$ 的正反压缩 SAM、对称压缩 SAM 和基本子串结构(图源:字符串技术巡礼):
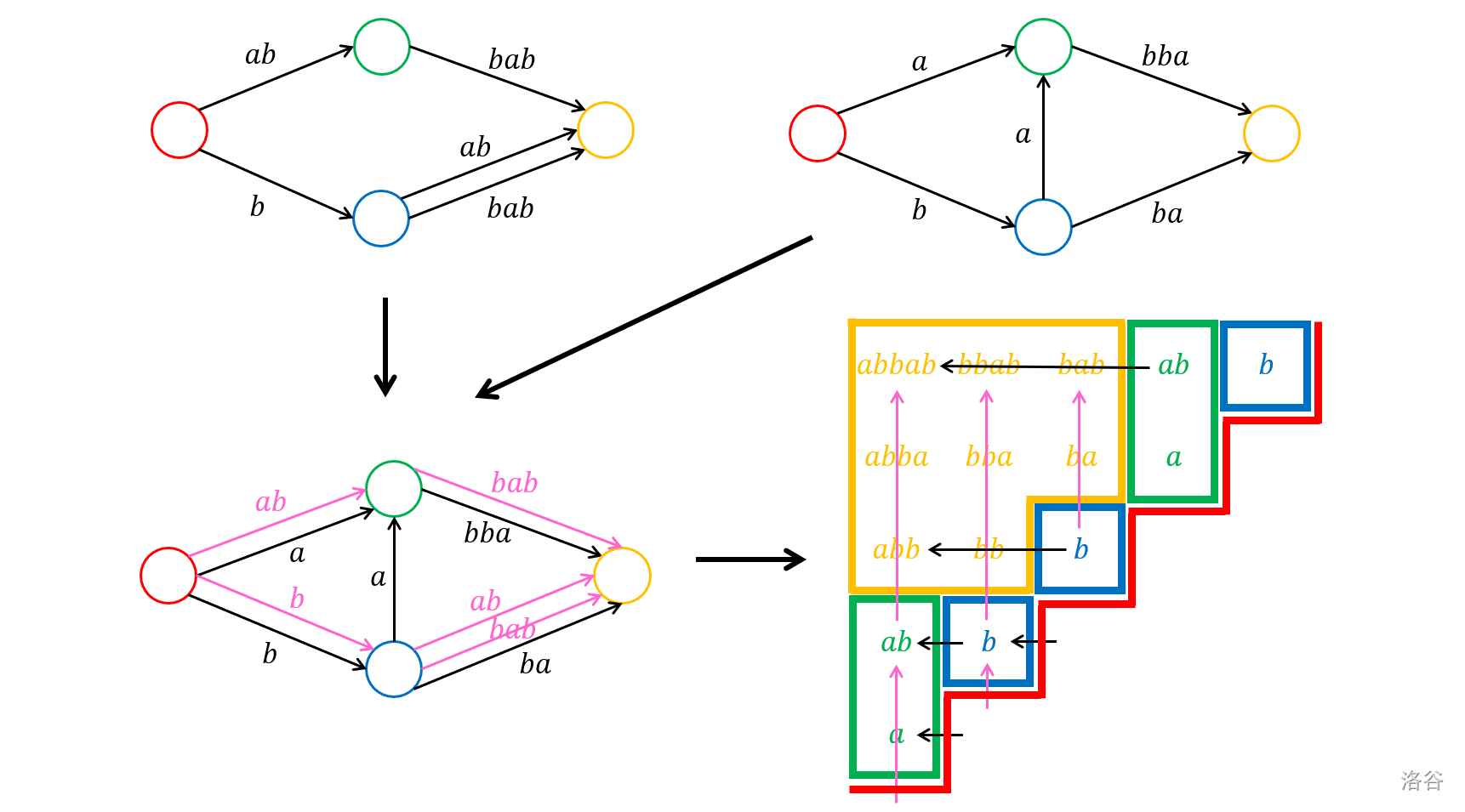
下面证明几个重要的性质:
Lemma 1. 每个块是一个阶梯状网格图,且上端和左端对齐。
证明:
- 首先考虑上端和左端对齐。假设块内有两个点 $(l_1,r_1)$ 和 $(l_2,r_2)$,那么这两个点的对应的 $\text{ext}$ 是相同的,并且与 $(\min(l_1,l_2),\max(r_1,r_2))$ 也相同。所以对于每一个块 $k$ 我们有最左上方的点(代表元) $\text{rep}(k)$,容易发现这个点对应的子串就是这个等价类对应的 $\text{ext}$。这个点唯一确定了块的上边界和左边界。
- “阶梯状”意味着对于 $l < l' \le r' < r$,都有 $(l'-1,r), (l',r+1), (l',r')$ 在同一块 $k$ 内,其中 $\text{rep}(k)=(l,r)$。这也是好理解的。
Lemma 2. 每个块 $k$ 恰好出现了 $\text{occ}(\text{rep}(k))$ 次。块内每个元素(在该块内)恰好出现了 $1$ 次。
证明从略。
Lemma 3. 每个块的每一行唯一对应正串 SAM 中的一个节点,每一列唯一对应反串 SAM 中的一个节点。
证明:注意到每一行对应一个 $\text{endpos}$ 等价类,且其不能向两边扩展。列的情况同理。
这个还引出了下一个重要推论:
Lemma 4. 所有本质不同的块的周长之和为 $O(|S|)$ 量级。
证明:由 Lemma 3 易推得。
DAG 无用论,树边标记
这里咕掉了若干个引理。
考虑走正串 SAM 的 DAG 边的过程:
- 如果不在等价类边界上,那么仅有一条出边,连向这个位置上方的位置;
- 否则,会连向所有反串 parent tree 上孩子节点的「对应位置」。
所以正反串的 parent tree 中包含了所有 DAG 的信息。
关于如何找到这个「对应位置」,我们有一种简洁的树边标记方法:
我们预处理出 SAM 上每个点 $i$ 对应 $\text{endpos}(i)$ 集合中的最小值,记为 $\text{pos}(i)$。
对于 $i\rightarrow \text{link}(i)$ 这条树边,我们可以马上知道 $\text{link}(i)$ 的最长串是通过加上 $S_{\text{pos}(i)-\text{len(link(}i))}$ 得到的!
因此扫一遍便完成了树边标记的任务。
构建算法
假设字符集大小 $\Sigma$ 为常数。
下面给出的是来自 Crashed 的做法而不是原论文做法。
- 构建正反串的 SAM。这个可以 $O(n)$ 做。
- 标记代表元。
注意到正串 SAM 上一个节点对应的最长字符串总是落在该块的左边界上。所以我们只需要把左边界对应的反串 SAM 节点拿出来(这是可以唯一确定的),比一比 $\text{len}_0(p)$ 和 $\text{len}_1(q)$ 就好了。
假设我们目前在 $p,q$ 这两个点上;我们枚举正 SAM 的 DAG 上出边,并且我们只走 $\text{len}_0(p')=\text{len}_0(p)+1$ 的出边,这样可以让我们一直在左边界上。
如果当前点不是代表元那么这样往上走是不会改变 $q$ 的;否则我们需要找到 $q$ 在 parent tree 上的哪个孩子是通过这个字符转移到的,这个可以通过上面提到的树边标记预处理。
(必要性证明先咕了。)
另外,如果不要求线性复杂度,我们也可以枚举正 SAM 中的每个节点,定位其第一次出现的位置,然后以一只 $\log$ 的代价找出其在反 SAM 上的对应节点,然后比较他们的 $\text{len}$;这样做的正确性比较显然。
- 划分等价类
我们按照 SAM 中 $\text{len}$ 从小往大的顺序扫一遍,如果一个点还未被归入某一个等价类就扫描他 DAG 上的的所有出边(符合条件的一定只有一条),并将其标记为 DAG 出边所指向的等价类。
另外,存在一种“按照 SAM 中编号从大往小扫描”的做法,正确性证明未知。
- 行列排序
神奇的事情是不用排,3 中倒着扫的时候顺带加入,就天然形成了倒序结构,所以最后形成的顺序就是行从上往下,列从左往右(因为本来是反串,再倒一次就形成了“正序”)。
(证明也咕了。)
应用与例题
对于本文开头提到的问题:
- 对于询问一,其实就是在询问等价类中,一个点左上方有几个子串(下图中蓝框)。
- 对于询问二,其实就是询问等价类中,一个点右下方有几个子串(红框)。
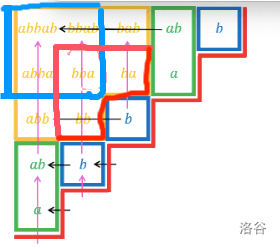
$$ \text{Fig 1. 询问子串为 bba 时,答案在网格图上的体现。} $$
随便拿个啥 DS 维护一下即可。